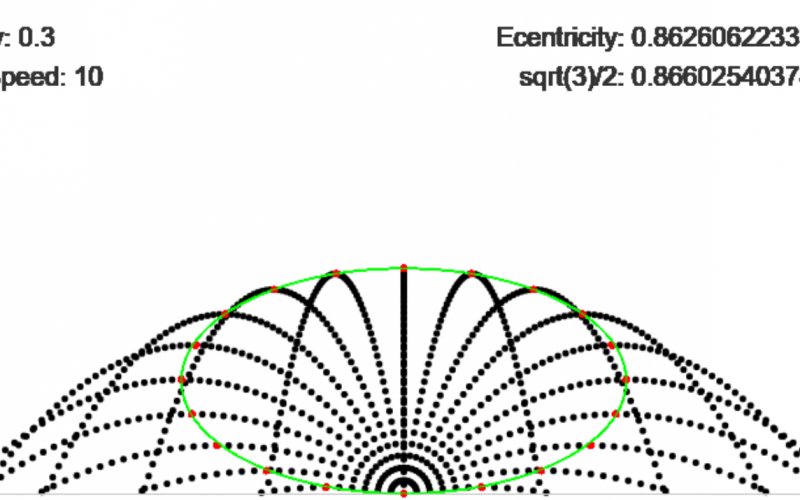
I wondered what shape you would get if you connected all the apex points of all trajectories, if you only changed the angle and kept the same initial speed. Surprisingly, you get an ellipse!The equation for the ellipse is:
x2 / a2 + (y – b)2 / b2 = 1
Where a = v02 / (2g) and b = v02 / (4g). v0 is the initial speed and g is the acceleration due to gravity. The eccentricity of this ellipse is constant for all values of v0 and g, and this value is e = √3 / 2. This sketch performs that simulation, and you can click to change the gravity and speed of the balls to a random new value: [raw] [/raw] Here is the code for the simulation.int n =21;
float gravity = 0.3;
float speed = 10;
void fire() {
if (frameCount != 0) {
//use 0.3 and 10 the first time, but random afterwards
speed = random(4, 10);
gravity = speed/10*random(.1, 1);
}
for (int i =0; i < n; i++) {
balls[i] = new Ball(i);
}
background(255);
}
void mousePressed() {
fire();
}
Ball[] balls = new Ball[n];
float floor;
class Ball {
PVector location;
PVector velocity;
PVector highestLocation;
float d = 5; //diameter
Ball(int number) {
//angles go from 0 to -PI
float angle = map(number * 1.0, 0, n-1, 0, -PI);
float speed = 10;
velocity = new PVector(speed, 0);
velocity.rotate(angle);
location = new PVector(width/2, floor);
highestLocation = new PVector(width/2, floor);
}
void move() {
location.add(velocity);
velocity.y += gravity;
if (location.y < highestLocation.y) {
highestLocation.x = location.x;
highestLocation.y = location.y;
}
}
void display() {
noStroke();
if (location.y < floor) { fill(0); ellipse(location.x, location.y, d, d); } if (location.y > highestLocation.y) {
fill(255, 0, 0);
ellipse(highestLocation.x, highestLocation.y, d, d);
}
}
}
void setup() {
size(800, 400);
floor = height - 30;
fire();
}
void draw() {
fill(50);
textSize(20);
textAlign(LEFT, TOP);
text("Gravity: "+gravity, 10, 10);
text("Start Speed: "+speed, 10, 40);
stroke(200);
line(0,floor,width,floor);
float highestY = height, circleTop = height, leftCircleX = width/2, rightCircleX = width/2;
for (Ball b : balls) {
b.move();
b.display();
if (b.location.y < highestY) {
highestY = b.location.y;
}
if (b.highestLocation.y < circleTop) {
circleTop = b.highestLocation.y;
}
if (b.highestLocation.x < leftCircleX) { leftCircleX = b.highestLocation.x; } if (b.highestLocation.x > rightCircleX) {
rightCircleX = b.highestLocation.x;
}
}
//Check if they have all fallen below floor
if (highestY >= floor) {
float centerX = width/2, centerY = (circleTop + floor)/2;
float circleHeight = floor - circleTop;
float circleWidth = rightCircleX - leftCircleX;
stroke(0, 255, 0);
noFill();
ellipse(centerX, centerY, circleWidth, circleHeight);
textAlign(RIGHT, TOP);
fill(50);
float eccentricity = sqrt(1-(circleHeight*circleHeight/(circleWidth*circleWidth)));
text("Ecentricity: "+eccentricity, width-10, 10);
text("sqrt(3)/2: "+sqrt(3)/2, width-10, 40);
}
}