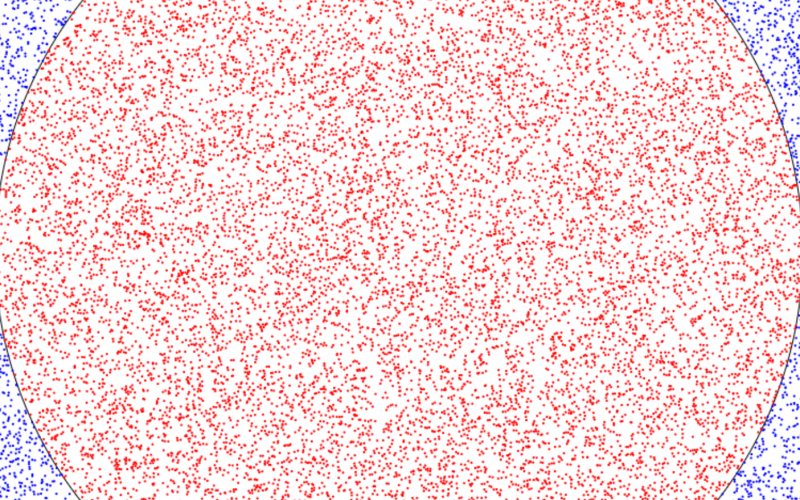
Pi, π, can be computed using Monte Carlo simulation. Although that may sound complicated, it’s simpler than it sounds: Generate random points within a square, and see how many of them are inside of the circle (with the same diameter as the square’s side).
A mathematical proof of the computation goes like this: We know the ratio of the circle’s area to the square’s area is π*r*r/(2*r*2*r), since the area of a circle is π*r*r and a square is length_of_side*length_of_side, or (2*r*2*r). That equation, ratio_of_circle_to_square = π*r*r/(2*r*2*r), simplifies to ratio_of_circle_to_square = π/4. And so ratio_of_circle_to_square * 4 is equal to π.
The following code performs that simulation. It draws 100 dots at a time, and counts how many of those dots are red. The number of red dots, divided by the total number of dots, times four, is pi!
Here is the code for the monte carlo simulation:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
float xmin,xmax,ymin,ymax,xcenter,ycenter,radius; int simsPerFrame = 10000; color inside = color(255,0,0), outside = color(0,0,255); int countIn = 0, countTotal = 0; void setup() { size(600,700); xmin = 0; ymin = 100; xmax = width; ymax = height; xcenter = width/2; ycenter = (ymax-ymin)/2 + ymin; radius = width/2; background(255); ellipse(xcenter,ycenter,radius*2,radius*2); } void draw() { fill(255); rect(0,0,width,ymin); for(int i = 0; i < simsPerFrame; i++) { float x = random(xmin,xmax); float y = random(ymin,ymax); boolean in = dist(x,y,xcenter,ycenter) <= radius; if(in) { fill(inside); countIn++; }else { fill(outside); } countTotal++; noStroke(); ellipse(x,y,2,2); } fill(0); textAlign(LEFT,TOP); textSize(15); double ratio = countIn; ratio /= countTotal; text("Points inside: "+countIn+", points total: "+countTotal,10,10); text("Ratio: "+ratio,10,40); text("4*Ratio, or estimated value of PI: "+ratio*4,10,70); } |