float xmin,xmax,ymin,ymax,xcenter,ycenter,radius;
int simsPerFrame = 10000;
color inside = color(255,0,0), outside = color(0,0,255);
int countIn = 0, countTotal = 0;
void setup() {
size(600,700);
xmin = 0;
ymin = 100;
xmax = width;
ymax = height;
xcenter = width/2;
ycenter = (ymax-ymin)/2 + ymin;
radius = width/2;
background(255);
ellipse(xcenter,ycenter,radius*2,radius*2);
}
void draw() {
fill(255);
rect(0,0,width,ymin);
for(int i = 0; i < simsPerFrame; i++) {
float x = random(xmin,xmax);
float y = random(ymin,ymax);
boolean in = dist(x,y,xcenter,ycenter) <= radius;
if(in) {
fill(inside);
countIn++;
}else {
fill(outside);
}
countTotal++;
noStroke();
ellipse(x,y,2,2);
}
fill(0);
textAlign(LEFT,TOP);
textSize(15);
double ratio = countIn;
ratio /= countTotal;
text("Points inside: "+countIn+", points total: "+countTotal,10,10);
text("Ratio: "+ratio,10,40);
text("4*Ratio, or estimated value of PI: "+ratio*4,10,70);
}
Estimating PI with Monte Carlo Simulation in Processing
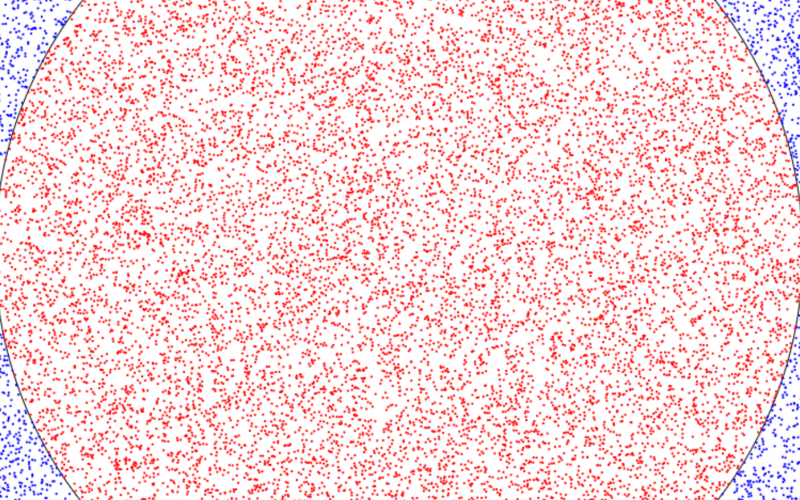
Pi, π, can be computed using Monte Carlo simulation. Although that may sound complicated, it’s simpler than it sounds: Generate random points within a square, and see how many of them are inside of the circle (with the same diameter as the square’s side).
A mathematical proof of the computation goes like this: We know the ratio of the circle’s area to the square’s area is π*r*r/(2*r*2*r), since the area of a circle is π*r*r and a square is length_of_side*length_of_side, or (2*r*2*r). That equation, ratio_of_circle_to_square = π*r*r/(2*r*2*r), simplifies to ratio_of_circle_to_square = π/4. And so ratio_of_circle_to_square * 4 is equal to π.
The following code performs that simulation. It draws 100 dots at a time, and counts how many of those dots are red. The number of red dots, divided by the total number of dots, times four, is pi!
[raw]
[/raw]
Here is the code for the monte carlo simulation: